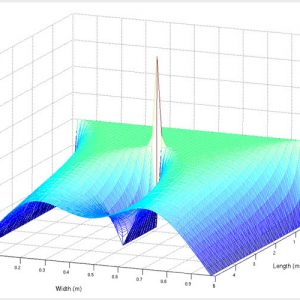
Бристольский ученый решил столетнюю физическую задачу – дискретное диффузное уравнение в конечном пространстве. Решение, которое давно искали, может быть полезным для точного прогнозирования вероятности встречи и передачи между людьми в замкнутой среде, без использования отнимающих время компьютерных моделирований.
В своей работе доктор Лука Джуджоли из отделения инженерной математики университета Бристоля описывает, как аналитически рассчитать вероятность прохождения (в дискретном времени и дискретном пространстве) диффузной частицы или единицы в замкнутом пространстве – это то, что до сих пор было возможно решить лишь с помощью вычислений, сообщает sciencedaily.
Доктор Джуджоли отметил: «Диффузное уравнение моделирует случайное движение и является одним из фундаментальных уравнений физики. Аналитическое решение диффузного уравнения в конечных областях, где время и пространство непрерывны, известно уже давно».
Однако, чтобы сравнить прогноз модели с эмпирическим наблюдением, следует изучить диффузное уравнение в конечном пространстве. Несмотря на работы выдающихся ученых в прошлом, до сих пор это оставалось нерешенной задачей больше века.
Читайте еще: Цифровой архив-анамнез жизни человека – новый тренд в телемедицине
«Приятно, что открытие именно этого аналитического решения позволяет нам найти подход к проблемам, которые ранее были практически неразрешимы из-за стоимости вычислений», – добавил он.
Результаты могут широко применяться в ряде дисциплин – прогнозирование диффузии молекул внутри клетки, передвижение бактерий в чашке Петри, передвижение животных по территории или роботов, движущихся на месте стихийного бедствия. Их также можно использовать для прогнозирования передачи патогена в толпе между людьми.

